Derivative関数の働き・役割
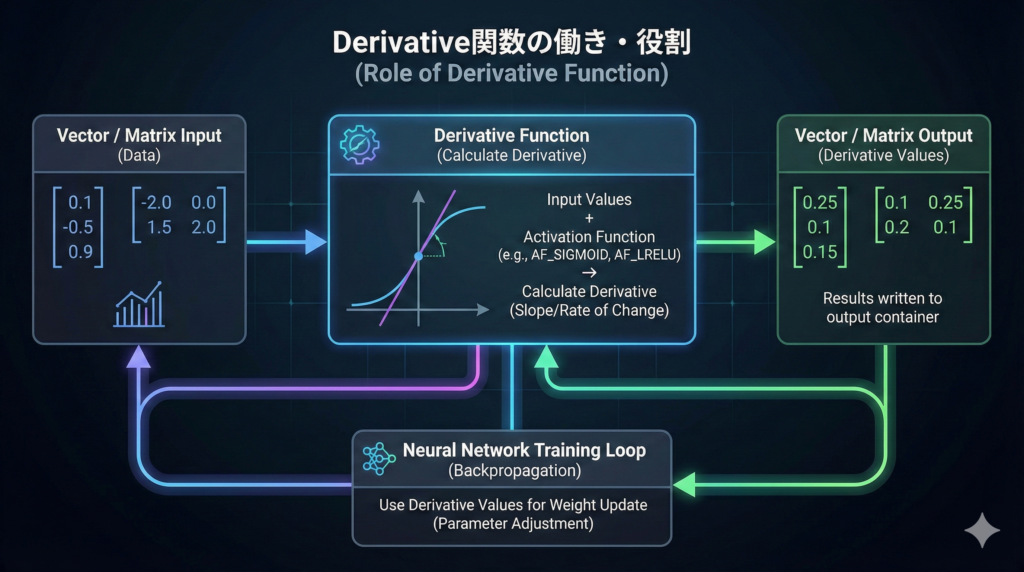
Derivative関数は、ベクトル(数値を1列に並べた入れ物)や行列(数値を縦横の表の形に並べた入れ物)に入っている値を元にして、指定した活性化関数(ニューラルネットワークで、入力値を別の形に変換する計算式)の導関数(入力が少し変わったとき、出力がどれくらい変わるかを表す値)を計算し、その結果を渡されたベクトルや行列に書き込みます。
誤差逆伝播(ニューラルネットワークで、出力のズレを元に重みを調整する計算)では、学習中に「その地点での導関数の値」を使ってパラメータを更新します。Derivative関数は、その更新に必要な導関数の値をまとめて計算して取り出すために用意されています。
Derivative関数の引数について
bool vector::Derivative(
vector& vect_out, // 値を取得するベクトル
ENUM_ACTIVATION_FUNCTION activation, // 活性化関数
... // 追加のパラメータ
);
bool matrix::Derivative(
matrix& matrix_out, // 値を取得する行列
ENUM_ACTIVATION_FUNCTION activation // 活性化関数
);
bool matrix::Derivative(
matrix& matrix_out, // 値を取得する行列
ENUM_ACTIVATION_FUNCTION activation, // 活性化関数
ENUM_MATRIX_AXIS axis, // 軸
... // 追加のパラメータ
);
vector型のDerivative関数の書式
bool vector::Derivative(
vector& vect_out, // 値を取得するベクトル
ENUM_ACTIVATION_FUNCTION activation, // 活性化関数
... // 追加のパラメータ
);第1引数(vect_out)について
第1引数のvect_outは出力用のベクトルです。Derivative関数が計算した「活性化関数の導関数の値」が、このvect_outに書き込まれます。引数の向きとしてはoutで、呼び出し側が結果を受け取る入れ物を用意して渡す形になります。
第2引数(activation)について
第2引数のactivationは、どの活性化関数の導関数を計算するかを指定する値です。ENUM_ACTIVATION_FUNCTION列挙体(決められた選択肢を名前で指定する仕組み)から選びます。引数の向きとしてはinで、計算ルールを指定するために渡します。
第3引数以降(追加のパラメータ)について
第3引数以降は追加のパラメータです。これは、指定した活性化関数が受け取る追加パラメータと同じ意味を持ちます。活性化関数によっては形を調整するための数値を受け取ることがあり、その場合はDerivative関数にも同じ値を渡して導関数を計算します。追加パラメータを指定しない場合は、その活性化関数に用意されている初期値が使用されます。
matrix型のDerivative関数の書式(軸指定なし)
bool matrix::Derivative(
matrix& matrix_out, // 値を取得する行列
ENUM_ACTIVATION_FUNCTION activation // 活性化関数
);
第1引数(matrix_out)について
第1引数のmatrix_outは出力用の行列です。Derivative関数が計算した「活性化関数の導関数の値」が、このmatrix_outに書き込まれます。引数の向きとしてはoutで、結果を書き込む入れ物として渡します。
第2引数(activation)について
第2引数のactivationは、導関数を計算する対象となる活性化関数を指定する値です。ENUM_ACTIVATION_FUNCTION列挙体から選んで渡します。引数の向きとしてはinで、計算の種類を決めるために指定します。
matrix型のDerivative関数の書式(軸指定あり)
bool matrix::Derivative(
matrix& matrix_out, // 値を取得する行列
ENUM_ACTIVATION_FUNCTION activation, // 活性化関数
ENUM_MATRIX_AXIS axis, // 軸
... // 追加のパラメータ
);第1引数(matrix_out)について
第1引数のmatrix_outは出力用の行列です。Derivative関数が計算した導関数の値が、このmatrix_outに書き込まれます。引数の向きとしてはoutです。
第2引数(activation)について
第2引数のactivationは、どの活性化関数の導関数を計算するかを指定する値です。ENUM_ACTIVATION_FUNCTION列挙体から選んで渡します。引数の向きとしてはinです。
第3引数(axis)について
第3引数のaxisは、ENUM_MATRIX_AXIS列挙体(行列のどちら方向を基準にするかを指定する選択肢)から軸を指定します。AXIS_HORZは水平軸、AXIS_VERTは垂直軸を表します。ここで指定した軸の解釈は、行列の中で「行に何を並べ、列に何を並べているか」というデータの並べ方と合わせて考える必要があります。引数の向きとしてはinです。
第4引数以降(追加のパラメータ)について
第4引数以降は追加のパラメータです。指定した活性化関数が追加のパラメータを受け取る場合に、その値をDerivative関数にも渡します。追加パラメータを省略した場合は、活性化関数側の初期値が使用されます。
Derivative関数の戻り値について
Derivative関数の戻り値はbool型(trueかfalseのどちらか)です。処理に成功した場合はtrueが返り、処理に失敗した場合はfalseが返ります。
trueが返ったときは、第1引数で渡したvect_outまたはmatrix_outに、指定した活性化関数の導関数の計算結果が書き込まれています。たとえば、呼び出し元のベクトルや行列に入っている各要素の値を入力として、その要素ごとの導関数値が同じ並びで出力側に入ります。
falseが返ったときは、導関数の計算結果が正しく書き込まれていない可能性があります。この場合は、出力先として渡したvect_outまたはmatrix_outの状態だけを前提に次の計算を進めず、引数の指定が適切だったか、追加パラメータが必要な活性化関数に対して値を渡していたかといった点を見直してから、再度呼び出す形にします。
Derivative関数を使ったサンプルコード
// このスクリプトは、Derivative関数の使い方を確認するための例です。
// 実行すると、ログ(ターミナルの「エキスパート」タブなど)に計算結果が表示されます。
// ここでは、vector型とmatrix型の両方でDerivative関数を使い、導関数の値が出力先に書き込まれる流れを見ます。
void OnStart()
{
// -------------------------------------------------------------------------
// 例1:vector型でDerivative関数を使う
// -------------------------------------------------------------------------
// vector型は、数値が1列に並んだデータです。
// ニューラルネットワークの計算では、複数の入力値をまとめて扱う場面が多いため、
// このような「まとめたデータ」に対して一括で計算できるようになっています。
// 入力となるベクトルを用意します。
// このxの中に入っている値が、Derivative関数が導関数を計算するときの「入力値」になります。
// 正の値、負の値、0を混ぜておくと、活性化関数によって結果がどう変わるかを確認しやすくなります。
vector x = { 0.1, 0.4, 0.9, 2.0, -5.0, 0.0, -0.1 };
// yは、Activation関数の計算結果を受け取るためのベクトルです。
// Activation関数は「活性化関数を適用した値」を計算して、このyに書き込みます。
vector y;
// dyは、Derivative関数の計算結果を受け取るためのベクトルです。
// Derivative関数は「活性化関数の導関数の値」を計算して、このdyに書き込みます。
// ここが今回の主役です。
vector dy;
// AF_LRELU(Leaky ReLU)には、追加パラメータとしてalphaを渡せます。
// alphaは、入力が負のときの傾き(変化の割合)を決める値です。
// ここでは0.1にしています。
// この値はActivation関数とDerivative関数で揃えて使う必要があります。
double alpha = 0.1;
// xの各要素に対して、AF_LRELUの活性化関数を適用します。
// 計算結果はyに書き込まれます。
// ここでのポイントは、Activation関数は戻り値として結果を返すのではなく、
// 「第1引数に渡した入れ物(ここではy)に書き込む」という形で結果を渡すことです。
x.Activation(y, AF_LRELU, alpha);
// xの各要素に対して、AF_LRELUの導関数(導関数の値)を計算します。
// 計算結果はdyに書き込まれます。
// ここでも、結果は戻り値ではなく、第1引数の入れ物(dy)に書き込まれます。
// そして、alphaはActivation関数で使った値と同じものを渡します。
x.Derivative(dy, AF_LRELU, alpha);
// ここからは、計算結果をログに表示して確認します。
// xは入力値そのものです。
// yはActivation関数を通した出力値です。
// dyはDerivative関数で計算した導関数の値です。
// この3つを並べて見ることで、「入力がこの値のとき、出力はこうで、導関数はこう」という対応を確認できます。
Print("x = ", x);
Print("y = ", y);
Print("dy = ", dy);
// -------------------------------------------------------------------------
// 例2:matrix型でDerivative関数を使う(軸指定なしの書式)
// -------------------------------------------------------------------------
// matrix型は、数値が縦横の表として並んだデータです。
// たとえば「行がデータのまとまり、列が特徴量」のように扱うことが多いです。
// ここでは単純な2行3列を用意して、行列全体に対して活性化関数と導関数を計算します。
// 2行3列の行列を作ります。
// 引数の(2, 3)は「行数が2、列数が3」を意味します。
matrix m(2, 3);
// 行列mの各要素に値を代入します。
// m[行][列]の形でアクセスします。
// ここも、負の値、0、正の値を混ぜています。
// そうすることで、活性化関数の反応が変わる部分を確認しやすくなります。
m[0][0] = -2.0; m[0][1] = -0.5; m[0][2] = 0.0;
m[1][0] = 0.5; m[1][1] = 1.0; m[1][2] = 2.0;
// myは、Activation関数の結果を受け取る行列です。
// mに活性化関数を適用した結果が、このmyに書き込まれます。
matrix my;
// dmyは、Derivative関数の結果を受け取る行列です。
// mの各要素に対する導関数の値が、このdmyに書き込まれます。
matrix dmy;
// mの各要素に対して、AF_SIGMOIDの活性化関数を適用します。
// AF_SIGMOIDは追加パラメータを渡さない形でも使える活性化関数の例です。
// 計算結果はmyに書き込まれます。
m.Activation(my, AF_SIGMOID);
// mの各要素に対して、AF_SIGMOIDの導関数の値を計算します。
// 計算結果はdmyに書き込まれます。
// ここでは軸指定なしの書式を使っており、行列の各要素ごとに導関数が計算されるイメージで確認できます。
m.Derivative(dmy, AF_SIGMOID);
// 行列は複数行になるので、見やすいように改行を入れて表示します。
// "m =\n" のように \n を入れると、ラベルの直後で改行されます。
// その後に行列を渡すと、行列の形で出力されます。
Print("m =\n", m);
Print("my =\n", my);
Print("dmy =\n", dmy);
// -------------------------------------------------------------------------
// まとめとして押さえるポイント
// -------------------------------------------------------------------------
// 1) Derivative関数は、呼び出し元(xやm)に入っている値を入力として導関数を計算します。
// 2) 結果は戻り値ではなく、第1引数で渡した出力先(dyやdmy)に書き込まれます。
// 3) 追加パラメータが必要な活性化関数では、Activation関数とDerivative関数で同じ値を渡します。
// 4) Printで入力・出力・導関数を並べて表示すると、対応関係を確認しやすくなります。
}
Derivative関数のサンプルコードに使われた関数や文法要素の簡単な解説
OnStart関数は、スクリプト(チャートに入れて一度だけ動かすプログラム)を実行した直後に呼ばれる関数です。このサンプルでは、ベクトルと行列の準備、Activation関数による計算、Derivative関数による計算、Print関数による確認までを、OnStart関数の中で上から順に実行しています。
vector型は、数値を1列に並べて持つ型です。サンプルのxという変数は、導関数を計算したい入力値そのものを入れておく場所になっています。ここで重要なのは、Derivative関数はvect_outに入っている値から導関数を作るのではなく、呼び出し元であるxに入っている値を入力として導関数を計算する点です。つまり、Derivative関数を呼ぶ直前のxの中身が、そのまま導関数の計算対象になります。
matrix型は、数値を縦横の表として持つ型です。サンプルのmという変数は2行3列として作り、m[0][0]のように行と列を指定して各要素に値を入れています。ここでもvector型と同じで、Derivative関数は呼び出し元のmに入っている値を入力として導関数を計算し、その結果を別の行列に書き込みます。
Activation関数は、指定した活性化関数を使って、呼び出し元の各要素を変換し、その結果を出力用の入れ物に書き込みます。サンプルでは、vector型のxに対してActivation関数を呼び出してyという変数に結果を書き込んでいます。同様に、matrix型のmに対してActivation関数を呼び出してmyという変数に結果を書き込んでいます。ここで押さえておきたい点は、Activation関数の計算結果は戻り値として受け取るのではなく、引数で渡したyやmyのような入れ物に書き込ませて受け取る設計になっていることです。
Derivative関数は、指定した活性化関数の導関数の値を計算し、出力用の入れ物に書き込みます。サンプルでは、vector型のxに対してDerivative関数を呼び出してdyという変数に書き込み、matrix型のmに対してDerivative関数を呼び出してdmyという変数に書き込んでいます。Activation関数と同様に、Derivative関数も戻り値で結果を返すのではなく、第1引数で渡した入れ物に書き込む形です。戻り値のbool型は、処理が成功したかどうかを表すためのものなので、結果そのものは必ずdyやdmy側を見て確認します。
AF_LRELUは、追加パラメータとしてalphaを受け取るタイプの活性化関数です。サンプルではalphaという変数を用意し、Activation関数とDerivative関数の両方に同じalphaを渡しています。ここがずれると、Activation関数で使った活性化関数の形と、Derivative関数で計算した導関数の形が一致しなくなり、学習の計算などで整合が取れなくなります。サンプルでalphaを明示しているのは、追加パラメータがある活性化関数では同じ値を渡す必要があることを、コード上で確認できるようにするためです。
AF_SIGMOIDは、追加パラメータを渡さない形でも使える活性化関数です。サンプルでは、行列の例でAF_SIGMOIDを使い、追加パラメータなしでActivation関数とDerivative関数を呼び出しています。追加パラメータを必要としない活性化関数では、このようにシンプルな呼び出しになります。
Print関数は、値をログに出すための関数です。サンプルでは、ベクトルの例でx、y、dyを順番に表示し、入力値、活性化関数の出力、導関数の値を並べて見られるようにしています。行列の例では、表示の前に改行を入れてから行列を出すことで、m、my、dmyが表の形で読みやすくなるようにしています。導関数の確認では、入力値と導関数の値をセットで見ると、どの入力で導関数がどう変化するかを追いやすくなります。
double型は、小数を含む数値を扱う型です。サンプルではalphaのように、活性化関数の形を調整する値としてdouble型を使っています。活性化関数の計算は小数を含むことが多いため、パラメータも小数で持てる型にしておくのが自然です。
変数の用意の仕方にも意図があります。xやmは入力側として固定し、yやmyはActivation関数の結果、dyやdmyはDerivative関数の結果という形で役割を分けています。こうしておくと、同じ入力に対して「活性化関数を通した結果」と「導関数の結果」を同時に保持できるため、ログで見比べるだけでなく、後続の計算に渡すときにも混乱しにくくなります。
Derivative関数を使ってEAを作る際のアイディア
EA(Expert Advisor。自動売買プログラム)に機械学習の考え方を取り入れる場合、Derivative関数は「学習の計算に必要な導関数の値」を用意する役割として使えます。たとえば、複数の入力特徴量(予測のために使う入力データ)をベクトルや行列にまとめ、重み(入力に掛ける係数)を通してスコアを作り、活性化関数で出力を作る流れをEAの中に組み込みます。学習を行うときは、出力と目標値の差から誤差を作り、その誤差を元に重みを更新しますが、その更新量を計算する途中で活性化関数の導関数が必要になります。Derivative関数で導関数の値をベクトルや行列として用意しておくと、更新計算を同じ形のデータのまま進めやすくなります。
取引シグナルの強さを表す値を作る場面でも、Derivative関数を間接的に役立てられます。たとえば、複数の条件を点数化して合計し、その合計を活性化関数で一定の範囲に収めて「買い寄りか売り寄りか」を表す数値にします。このとき、導関数の値が大きい入力帯は、入力が少し変わるだけで出力が大きく動きやすい帯です。導関数の値を見ながら、出力が敏感になりすぎている局面では発注を控える、あるいはロットを抑えるといった制御を入れる設計ができます。出力だけを見るのではなく「出力がどれくらい動きやすい状態か」も数値で持てるのが、導関数を計算する意味になります。
複数の通貨ペアや複数の時間足を同時に評価するEAでも、Derivative関数のまとめ計算が活かせます。たとえば、通貨ペアごとの特徴量を行列の各行に並べ、各列に同じ種類の特徴量をそろえて格納します。行列の形のままActivation関数で出力行列を作り、同じ入力行列に対してDerivative関数で導関数行列を作っておくと、通貨ペアごとに同じ処理を繰り返して書くのではなく、行列の計算として揃えた形で扱えます。結果として、通貨ペアの数が増えても処理の書き方が変わりにくく、評価と更新の流れを同じ設計で保ちやすくなります。
学習まで行わないEAでも、パラメータ調整のヒントとして導関数を使う考え方があります。たとえば、シグナル計算に使う活性化関数のパラメータを変えると、出力の変化のしかたが変わります。バックテスト(過去データで動作を検証すること)で、出力が急に切り替わりすぎてエントリーが多くなりすぎる場合は、入力の分布と導関数の大きさをセットで観察し、どの入力帯で出力が過敏になっているかを確認してから、パラメータや前処理の調整につなげる形が考えられます。導関数の値は、出力の見た目だけでは分かりにくい「変化のしやすさ」を捉える材料になります。