<PR＞-
当サイトでは以下のFX業者をおススメいたします。
標準偏差とは？-はじめに-
標準偏差は、データの「ばらつき」の大きさを表す統計学的な指標です。
標準偏差という言葉自体は割と聞き馴染みがあるかと思いますが、その本質的な意味を問われると、意外と「？」となってしまう方もいるのではないでしょうか？
「そもそもばらつきってなに？」という事も、改めて考えてみると意外と言語化するのが難しかったりもします。
この記事では、標準偏差を理解する為に必要な「ばらつき」「平均」「分散」「平方根」といった概念も併せて丁寧な解説を行い、初心者の方にも標準偏差が無理なく理解できるような構成を心掛けました。
この記事を読めば、標準偏差についてばっちり理解する事ができます。是非楽しんでお読みください。
「ばらつき」とは？
標準偏差はデータの「ばらつき」の大きさを表す指標である、という事を一番最初に書きましたが、まずはそもそも「ばらつき」とは何か？という点について、考えてみましょう。
「ばらつき」とは、データが平均値からどれだけ離れて分布しているかを示す指標です。
別の言い方をすると、「ばらつき」とはデータの値が平均値の周りに密集しているか、それとも広範囲に散らばっているかを表している、とも言えます。
偏差とは？
そもそも標準偏差の「偏差」とは、それぞれのデータが平均からどれくらい「ばらついているか」というものを数値化したものです。
今回の記事の主役である標準偏差は各データの偏差を平均化したものとなります。
定義としては「ばらつき」と同じような説明になりますが、
「ばらつき」がデータ全体のちらばり度合いを指す、より一般的な表現であるのに対し、偏差は具体的に1つ1つのデータがが具体的に平均値からどれだけ離れているかを示す値という事になります。
では、偏差の具体例をこれから見ていきましょう。
偏差の具体例
仮に、5人の生徒がテストを受け、次のようなスコアを得たとします。
- 生徒A: 80点
- 生徒B: 90点
- 生徒C: 85点
- 生徒D: 95点
- 生徒E: 75点
これらのスコアの平均値を計算すると、
平均=（80+90+85+95+75）/5=85点 となります。
次に、各生徒のスコアが平均からどれだけ離れているか、つまり偏差を計算します。生徒A～Eの偏差は以下のようになります。
生徒Aと生徒Eは平均より低く、生徒Bと生徒Dは平均より高いスコアです。
生徒Cはちょうど平均です。
このように偏差は、それぞれのデータが集団の平均からどれだけ「離れている」かを示す個々の値として理解できます。標準偏差はこれらの偏差を使って計算される事になります。
※標準偏差の詳しい計算式などはこの後じっくり解説しますので、今はぼんやりとした理解で大丈夫です。
※一応平均についても↓にて言及しておきます。
平均とは？
平均とは、極めて簡潔に言うと、全データの合計をデータの数で割った結果の値を言います。
平均の計算例
仮に、5人の生徒のテストスコアが以下のようになっているとします。
- 生徒A: 80点
- 生徒B: 90点
- 生徒C: 85点
- 生徒D: 95点
- 生徒E: 75点
これらのスコアの平均を計算するには、すべてのスコアを合計して、スコアの総数（この場合は生徒の数、5人）で割ります。
1：スコアの合計を計算する→ 80 + 90 + 85 + 95 + 75 = 425
2：スコアの合計を生徒の数で割る→ 425 ÷ 5 = 85
したがって、この5人の生徒のテストスコアの平均は85点、という事になります。
標準偏差についての、ここまでのまとめ
標準偏差を理解するにあたり、まずは標準偏差が「ばらつき」をあらわすもの、
そして「ばらつき」とは（主にデータ全体の）「平均」からの距離を表現する言葉であるという事、
そして「偏差」とは、それぞれ個々のデータが平均からどれくらい「ばらついているか」というものを数値化したもの
という事を覚えておいてください。
「平均」「ばらつき」「偏差」という標準偏差を理解する為の基本概念を押さえたところで、標準偏差に立ち戻ります。
大事な点なので改めて言いますが、標準偏差は「ばらつき」の程度を数値化したものとなります。
ばらつきが小さいほどデータの値は平均値に近く集まっており、大きいほど平均値から離れて広がっています。
そして、標準偏差が大きい場合、各データのばらつきが大きいことを意味し、小さい場合は各データが平均値に近い値を取っていることを意味します。
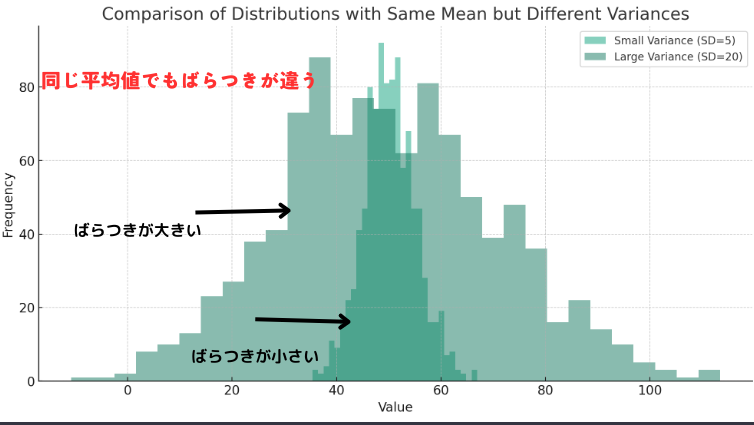
↑のヒストグラムでは、同じ平均値（50）を持つ2つのデータセット（関連するデータの集まり）を比較しています。
一方のデータセットには小さな標準偏差（5）が、もう一方には大きな標準偏差（20）が設定されています。
ヒストグラムから明らかなように、小さな標準偏差を持つデータは平均値の周りに密集して分布しており、大きな標準偏差を持つデータはより広範囲に分布していることがわかります。
標準偏差の計算方法
標準偏差の計算式は以下のようになります↓
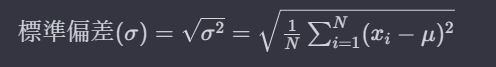
↑の式だけを見ると「うわ・・・」と思ってしまうかもしれませんが、↑の式の意味はこれから順を追って説明していきますので心配しないでください。
まずは身構えずに「こういうものなんだ」ぐらいに思っていただければ大丈夫です。
標準偏差の計算には、次のステップを踏んで行われます。
ステップ1：平均値の計算
まず、データの平均値（全データの合計をデータの数で割ったもの）を計算します。
ステップ2：各データと平均値の差の計算
次に、各データ点が平均値からどれだけ離れているかを計算します。これは、各データ点から平均値を引いて求めます。
ステップ3：差の二乗の計算
各データ点と平均値の差（=引き算した結果）を二乗（＝同じ数を２個掛け算する）します(なぜ二乗するのかはこの後説明します)
ステップ４：二乗した差の平均値の計算
これらの値(各データ点と平均値との差を二乗した値)の平均値を計算します。
※なお、この値の事を分散と呼びます。
分散とは？
分散は、各数値が平均からどれだけ離れているかを示す計算結果です。
標準偏差はこの分散の値を平方根に直したものになりますから、分散は標準偏差の前処理段階の値という事になります。
分散まず、各データの数値と平均の差を求め、その差の二乗を計算します。そして、その二乗した値の平均が分散です。これにより数値の散らばり具合を測定できます。
上記の分散の説明を計算式に落とし込むと以下のようになります↓
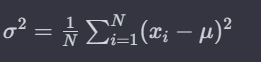
ここで、∑（シグマ）は各データの合計を表し、xiは各データ点、μ（ミュー）は対象データの平均値、Nはデータ点の数を意味します。
分散の具体的な計算例
例えば、データが[2, 4, 6]の場合、平均は4です。分散は、(2-4)² + (4-4)² + (6-4)² の総和をデータの数3で割り、計算します。これにより、データのばらつきの平均的な大きさを示す値が得られます。
答えとなる分散の値は約2.67となります。
なぜ分散を求める時に各データ点と平均との差を二乗するのか？
分散を求める時に各データ点と平均との差を二乗する理由なのですが、
単に各データ点と平均との差を合計しただけだと、正の差と負の差が相殺してしまい、実際の散らばりが正確に表されません。
たとえば、あるデータ点が平均よりも大きく、別のデータ点が平均よりも小さい場合、これらの差をそのまま足すとゼロになる可能性があります。
これでは、データが平均からどの程度離れているかを正しく評価できません。
「分散の具体的な計算例」セクションで使ったデータセット [2, 4, 6] を再び例として見てみましょう。
まず、このデータセットの平均を計算してみます。↓
平均=（2+4+6）/3=4
ここで、偏差をそのまま足し合わせてみると、
−2+0+2=0
となり、全体のばらつきがゼロに見えてしまいます。
これは、データが平均から離れている方向が異なる（一部は平均より上、一部は平均より下）ため、正と負の偏差が相殺されてしまうためです。
しかし実際には、データにはばらつきがあります。
そこで、各データ点と平均との差を二乗することによって、この問題を解決します。差を二乗すると、すべての値が正になるので、相殺されることがなくなります。
↑のデータを合計してデータ点の数で割ることで分散を求める、という事は既に説明した通りです。
このようにデータのばらつきにおける、正と負の影響を排除する事が、偏差を二乗することの主な理由です。
ステップ５：平方根の計算
最後に、分散の平方根を取ることで、ようやく標準偏差の値を得ることができます。
平方根についてはこの後すぐに解説します。
平方根とは？
平方根は、端的に言えばある数を二回掛けると元の数になる数です。
例えば、
2を2回掛けると4になるので、4の平方根は2、
3を2回掛けると9になるので、の平方根は3、
こんな感じです。
標準偏差の計算の具体例
ここまで標準偏差の計算過程と、それに必要な概念である
について解説を行ってきました。もしかしたら、ここまでの説明で疲れてしまった方もいるかもしれません。
各概念ごとのページ内リンクを細かく貼っていますので、わからない所があればそこに立ち返ってまた読んで頂ければと思います。
さて、それでは標準偏差の計算例を見ていきましょう。
5人の生徒のテストスコアがそれぞれ 70点、80点、90点、60点、100点だったとします。
- 平均値の計算: (70+80+90+60+100)/5=80 点
- 各データと平均値の差の計算:
- 70点の生徒：70−80=−10
- 80点の生徒：80−80=0
- 90点の生徒：90−80=10
- 60点の生徒：60−80=−20
- 100点の生徒：100−80=20
- 差の二乗の計算:
- 70点の生徒：(−10)2=100
- 80点の生徒：(0)2=0
- 90点の生徒：(10)2=100
- 60点の生徒：(−20)2=400
- 100点の生徒：(20)2=400
- 二乗した差の平均値の計算（＝分散を算出する）: (100+0+100+400+400)/5=200
- 分散の平方根の計算（標準偏差）: 200≈14.14
したがって、このテストスコアの標準偏差は約14.14点です。
これは、生徒のスコアが平均点の80点から平均的に約14点離れていることを意味します。標準偏差が小さいほど、生徒のスコアは平均に近く集まっています。
逆に、標準偏差が大きいほど、スコアは平均から遠くにばらついています。
標準偏差の計算でデータ点と平均値の差を二乗する理由
標準偏差の計算でデータ点と平均値の差を二乗する理由なのですが、以下のような理由があります。
正と負の差を打ち消さないため: データ点が平均値より大きい場合はプラスの差が、小さい場合はマイナスの差が生じます。単純にこれらを合計すると、プラスとマイナスが相殺されてしまい、実際のばらつきが適切に反映されません。
例えば、あるテストの点数が次のようになっているとします：• 生徒A: 70点（平均点から10点高い） • 生徒B: 50点（平均点から10点低い） • 平均点: 60点
2乗せずに差を計算すると、生徒Aの点数は平均から「+10」点、生徒Bの点数は平均から「-10」点です。この場合、差を単純に合計すると、+10と-10が打ち消し合い、合計差は0になってしまいます（+10 – 10 = 0）。
これでは、テストの点数に実際のばらつきがあるにもかかわらず、平均からのばらつきが一切ないかのように見えてしまいます。
このように、2乗しないと正と負の差が相殺されてしまい、実際のデータのばらつきを適切に反映できなくなるのです。
そのため、標準偏差を計算する際には、差を二乗してばらつきを正確に捉える必要があります。
実際に、差を二乗して計算すると、生徒Aと生徒Bの差はそれぞれ「100」となります（(70 – 60)² = 100、(50 – 60)² = 100）。
このように、差を二乗することで、すべての差を正の数に変換し、この問題を避ける事が出来るという訳です。
分散の値から平方根を求める理由
もう一つ重要な論点として、ばらつきの度合いを測るために算出した分散の値から何故平方根を求めるのか？」という問題があります。
標準偏差を求める際に分散の平方根を算出する理由は、データの散らばりを元の単位で表現するためです。
復習ですが、分散とは各データ点と平均値の差を二乗したものの平均です。
当然元のデータよりも数字が大きくなっている訳で、このままだと直感的に理解がしづらいです。100点満点のテストなのにばらつきが100というのは混乱の元ですよね。
従って、これを元のデータの単位に戻す必要があります。
平方根の利用: 分散の平方根を取ることで、二乗された単位を元の単位に戻すことができます。これにより、データの散らばりを元の単位で表現したものが標準偏差になります。
したがって、標準偏差は分散の平方根として算出され、データのばらつきを元の単位で理解しやすくするために使用されます。
２シグマ、３シグマについて
ここまで、標準偏差の基本的な解説をしてきましたが、この基本的な計算手順はあくまでも１シグマのものです。
２シグマとは?
１シグマ（「標準偏差の計算方法」セクションを参照）に対して、２シグマ（2σ）は、平均から±2倍の標準偏差の範囲を指します。
数学的には↓のように表されます。
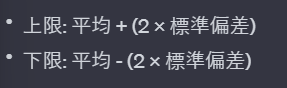
3シグマとは?
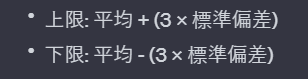
１シグマに対して、３シグマ（3σ）は、平均から±3倍の標準偏差の範囲を指します。
数学的には↓のように表されます。
2シグマ・３シグマの計算具体例
データセットが次のように与えられたとします。
このように２シグマも３シグマも、データがどの程度散らばっているかを示すものであり、２シグマも３シグマも標準偏差の１つです。
1シグマ、2シグマ、3シグマの範囲内にデータが収まる確率について
正規分布のデータにおいて、１シグマ、２シグマ、３シグマの各標準偏差範囲内にデータが収まる確率については、
- １シグマ（1σ）: 約68.27%のデータが平均値の±1標準偏差の範囲内に収まります。
- ２シグマ（2σ）: 約95.45%のデータが平均値の±2標準偏差の範囲内に収まります。
- ３シグマ（3σ）: 約99.73%のデータが平均値の±3標準偏差の範囲内に収まります。
正規分布について
「正規分布」は、データが平均値を中心にして左右対称のベル型の形で分布する現象を指します。
分布とは？
※「分布する」とは、データや物がある領域や集団の中でどのように広がっているかを表す言葉です。単に「存在する」よりも、もっとその配置や割合に焦点を当てた表現になります。
つまり、正規分布とは「データが平均値を中心に左右対称の形でデータが配置されている状態」という事になります。
多くのケースで、データの大部分は平均値の近くに集まり、平均から遠くなるにつれて少なくなります。この分布は自然界や人間の行動における多くの現象に当てはまります。
標準偏差を使う意味
そもそも、なぜ標準偏差は使われるのでしょうか？
標準偏差はばらつきを確認する指標である事は説明しましたが、そもそも平均からのばらつきを確認する事の意味はなんでしょうか？
ばらつきという言葉にピンとこない場合、「振り幅」という事に置き換えても構いません。
例えば、FXや株式の価格が平均から大きくばらつくと、振り幅が大きい→高リスク、平均からのばらつきが小さければ低リスクと見なされます。
振り幅が大きい→高リスクであることは大きな損失を被る可能性がある一方で、大きな利益を見込める可能性も秘めています。
反対に振り幅が小さい→低リスクであることは損失が限定的である一方で、利益の見込みも限定的であることを示唆しています。
つまり、上記のような投資におけるリスクを前提にしてリスクを可視化し、自分の資産に対して、どの程度のリスクであれば受け入れられるのか？という戦略を立てる上で、そのリスクを見積もる判断基準として標準偏差は大変便利になってくるわけです。
また投資対象の価格変動幅とその標準偏差を分析することで、市場の動向をある程度の確度をもって理解することができます。
例えば、大きな政治的イベントや経済指標の発表があると、市場のボラティリティ（=変動幅）は通常時よりも高まります。各経済指標発表時における価格変動幅と標準偏差、それ以外の通常時における価格変動幅その標準偏差の違いを、データとして比較検討する事で投資戦略を立てることも可能になります。
このように標準偏差を理解し、分析ツールとして使いこなせるようになる事にはFXでの利益を最大化する鍵が包摂されていると言えます。
特にこのブログはプログラミング言語MQL5・トレードソフトMT5などを使ったシステムトレードに関する情報を多く提供しています。
例えば、MT5でも組み込みインジケータとして提供されているボリンジャーバンドという指標は、中央の移動平均線と、その移動平均線から上下2本に描画された標準偏差で形成されているマルチバッファインジケータです。つまり、標準偏差を理解していないとボリンジャーバンドが提供する情報を正しく読み解く事ができない、という事になります。
またEA（エキスパートアドバイザーという自動売買プログラム）などの、開発したトレードシステムの性能を検証するにあたって、統計の基礎である標準偏差を正しく理解する事は最重要事項といっても過言ではありません。
今回の記事でしっかり学習し、今後のシステムトレードやバックテストなどの検証作業に活かして頂ければ幸いです。
※ボリンジャーバンドについては↓のリンクをご覧ください。
※移動平均線については↓の記事をご参照ください。
まとめ
今回の記事では標準偏差について解説しました。
まずは、標準偏差は、データのばらつきの大きさを表す統計学的な指標である、という大前提をお伝えした上で、標準偏差を理解する為に必要な「ばらつき」「平均」「分散」といった概念についての解説を行いました。
その前提を踏まえた上で、標準偏差の具体的な計算方法を具体例を挙げて説明しました。
※詳しくは「標準偏差の計算方法」セクションをご覧ください。
計算式の説明後は、
「なぜ分散を求める時に各データ点と平均との差を二乗するのか？」
といった、標準偏差を求める過程で生まれやすい疑問について、解説を行いました。詳しくは↑それぞれの記事内リンクをクリックして頂ければと思います。
そして、「標準偏差の計算方法」セクションで紹介した計算により求まった値は、あくまで１シグマのものであり、求まった値を２倍した２シグマ、３倍した３シグマも含めて標準偏差である事をお伝えしました。
※詳しくは「２シグマ、３シグマについて」セクションをご覧ください。
そして、最後に１シグマ、２シグマ、３シグマの範囲内にデータが収まる確率についても解説を行いました。収束する確率については以下の通りです。
- １シグマ（1σ）: 約68.27%のデータが平均値の±1標準偏差の範囲内に収まります。
- ２シグマ（2σ）: 約95.45%のデータが平均値の±2標準偏差の範囲内に収まります。
- ３シグマ（3σ）: 約99.73%のデータが平均値の±3標準偏差の範囲内に収まります。
今回は以上とさせていただきます。
最後までお読みいただきありがとうございました。
—————————————————————
-<PR＞-
MQL5を使って自作したEAをシステムトレードに利用するには、取引プラットフォームとしてMT5を提供しているFX会社に口座を開設しなくてはいけません。
当サイトでは以下のFX会社での口座開設・EA運用をおススメしています。
おススメする理由の詳細につきましては、各FX会社について解説する記事を書いておりますので、下記のリンク記事を参考にしていただければと思います。
※外為ファイネストに関する記事は↓をご覧ください。
※アヴァトレードジャパンに関する記事は↓をご覧ください。
