OnTester関数について解説した記事内↓にて、
OnTester関数を利用したサンプルコードも掲載しているのですが、同じ記事内で解説するには、ちょっと長くて複雑だったもので、別記事にして数回に分けて解説しています。
前回は「利益/損失情報を配列に格納する関数」について解説しました↓
今回は、「線形回帰を計算する関数」について解説します。
※線形回帰は、データの間の関係を見つけるための数学の方法です。
たとえば、身長と体重の関係を調べるときに、データの点をつなぐ最も良い直線を見つけて、その直線を使って「この身長の人はこのくらいの体重になるだろう」と予測することができます。
簡単に言うと、たくさんのデータを見て、それに一番合う直線を引いて、その直線を使って新しいデータを予測する方法です。線形回帰についての詳細は↓の動画もご参照ください。
解説するのは以下の箇所です↓
//+------------------------------------------------------------------+
//| 線形回帰を計算する y=a*x+b |
//+------------------------------------------------------------------+
bool CalculateLinearRegression(double &change[], double &chartline[], double &a_coef, double &b_coef)
{
//--- データが十分か確認する
if (ArraySize(change) < 3)
return (false);
//--- 蓄積されたチャート配列を作成する
int N = ArraySize(change);
ArrayResize(chartline, N);
chartline[0] = change[0];
for (int i = 1; i < N; i++)
chartline[i] = chartline[i - 1] + change[i];
//--- 線形回帰を計算する
double x = 0, y = 0, x2 = 0, xy = 0;
for (int i = 0; i < N; i++)
{
x = x + i;
y = y + chartline[i];
xy = xy + i * chartline[i];
x2 = x2 + i * i;
}
a_coef = (N * xy - x * y) / (N * x2 - x * x); // 傾きaを計算する
b_coef = (y - a_coef * x) / N; // 切片bを計算する
//--- 成功を示す
return (true);
}「線形回帰を計算する関数」の解説その1
このセクションでは、線形回帰を計算するための関数であるCalculateLinearRegression関数の一部について解説します。この関数は、データセットに基づいて線形回帰直線を計算し、傾きと切片を求める役割を果たします。
関数の概要
CalculateLinearRegression関数は、与えられたデータセットに基づいて線形回帰直線を計算し、回帰直線の傾きと切片を求めます。線形回帰直線は、データポイント間の関係を表す最も適合する直線です。
データが十分か確認する
//+------------------------------------------------------------------+
//| 線形回帰を計算する y=a*x+b |
//+------------------------------------------------------------------+
bool CalculateLinearRegression(double &change[], double &chartline[], double &a_coef, double &b_coef)
{
//--- データが十分か確認する
if (ArraySize(change) < 3)
return (false);まず、関数のヘッダ部分で、この関数が線形回帰を計算するものであることが示されています。この関数の引数は以下の通りです:
関数の冒頭で、データが十分かどうかを確認します。具体的には、変化量のデータセット(change配列)のサイズが3未満である場合、線形回帰を計算するためのデータが不十分と判断し、falseを返して関数を終了します。これは、少なくとも3つのデータポイントがないと信頼できる回帰直線を計算できないためです。
このように、CalculateLinearRegression関数は、与えられたデータセットに基づいて線形回帰直線を計算する前に、データが十分であることを確認する重要なチェックを行います。次に、十分なデータがある場合の計算処理について解説します。
「線形回帰を計算する関数」の解説その2
このセクションでは、線形回帰を計算するための関数であるCalculateLinearRegression関数の続きについて解説します。具体的には、蓄積されたチャート配列を作成する部分について説明します。
蓄積されたチャート配列を作成する
//--- 蓄積されたチャート配列を作成する
int N = ArraySize(change);
ArrayResize(chartline, N);
chartline[0] = change[0];
for (int i = 1; i < N; i++)
chartline[i] = chartline[i - 1] + change[i];データのサイズを取得し配列をリサイズする
まず、change配列のサイズを取得し、Nに格納します。次に、ArrayResize関数を使用して、chartline配列のサイズをNにリサイズします。これにより、chartline配列がchange配列と同じサイズになります。
※chartline配列とchange配列のサイズをそろえる理由は、両方の配列が対応するデータポイント(それぞれのデータの位置にある値)を持つ必要があるためです。サイズが一致していないと、正確に対応するデータポイントを保持できません。
サイズを一致させることで、forループ内での計算が一貫して行われ、chartline配列の各要素がchange配列の対応する要素の累積値(各時点までのデータの合計)を持つことが保証されます。
初期値の設定と累積値の計算
次に、chartline配列の初期値を設定します。chartlineの最初の要素にchange配列の最初の要素を設定します。これは、累積値の計算の起点となります。
※chartlineの最初の要素にchange配列の最初の要素を設定する理由は、累積値の計算を正しく行うための基準点を設定するためです。
基準点は、まず
chartline[0] = change[0]
となり、次の要素から累積値を計算できます。
例えば、次の要素はchartline[1] = chartline[0] + change[1]となります。
累積値の計算
forループを使用して、chartline配列の残りの要素を計算します。具体的には、chartlineの現在の要素に、前の要素の値にchange配列の現在の要素の値を加算します。これにより、chartline配列には累積値が格納されます。
この処理により、蓄積されたチャート配列が作成され、線形回帰を計算するための準備が整います。次に、回帰直線の計算に進みます。
「線形回帰を計算する関数」の解説その3
このセクションでは、線形回帰を計算するための関数であるCalculateLinearRegression関数の続きについて解説します。具体的には、線形回帰の計算部分について説明します。
線形回帰の計算
//--- 線形回帰を計算する
double x = 0, y = 0, x2 = 0, xy = 0;
for (int i = 0; i < N; i++)
{
x = x + i;
y = y + chartline[i];
xy = xy + i * chartline[i];
x2 = x2 + i * i;
}
線形回帰の計算式について
線形回帰の目的は、データセットに最も適合する直線(回帰直線)を求めることです。この直線は次の形式で表されます: y=a⋅x+b
ここで、
線形回帰の計算には、以下の数式が用いられます:
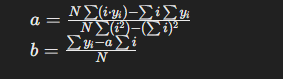
ここで、
変数の初期化と累積計算
この部分のコードでは、線形回帰の計算に必要な変数を初期化し、累積計算を行います。
- 変数の初期化:
- 累積計算:
- xを累積します。
- yを累積します。
- xyを累積します。
- x2を累積します。
この累積計算によって、線形回帰の計算に必要なすべての変数が準備されます。次に、これらの変数を用いて回帰直線の傾きと切片を計算します。
「線形回帰を計算する関数」の解説その4
このセクションでは、線形回帰を計算するための関数であるCalculateLinearRegression関数の続きについて解説します。具体的には、回帰直線の傾きと切片を計算し、関数の成功を示す部分について説明します。
回帰直線の傾きと切片を計算する
a_coef = (N * xy - x * y) / (N * x2 - x * x); // 傾きaを計算する
b_coef = (y - a_coef * x) / N; // 切片bを計算する
//--- 成功を示す
return (true);
}
傾きと切片の計算式
ここでは、線形回帰の計算式を用いて、回帰直線の傾きaと切片bを計算します。
- 傾きaの計算:
- 傾きaは次の式で計算されます:
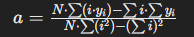
- この式に基づき、コードでは次のように計算しています:
a_coef=(N∗xy−x∗y)/(N∗x2−x∗x)
切片bの計算:
- 切片bは次の式で計算されます:
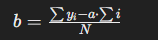
-
- この式に基づき、コードでは次のように計算しています: b_coef=(y−a_coef∗x)/Nb\_coef = (y – a\_coef * x) / Nb_coef=(y−a_coef∗x)/N
計算の成功を示す
傾きと切片の計算が完了した後、関数はtrueを返して成功を示します。これにより、CalculateLinearRegression関数が正常に実行され、回帰直線の傾きと切片が正しく計算されたことがわかります。
このように、CalculateLinearRegression関数は、データセットに基づいて回帰直線の傾きと切片を計算し、成功を示す役割を果たします。この計算により、データの傾向を表す直線が求められ、データ分析に役立てられます。
OnTester関数を使ったサンプルコードの全体記述
//-- 取引操作クラスをインクルードする
#include <Trade\Trade.mqh>
//--- EA入力パラメータ
input double Lots = 0.1; // ロット数(取引量)
input int Slippage = 10; // 許容されるスリッページ(価格変動幅)
input int MovingPeriod = 80; // 移動平均の期間
input int MovingShift = 6; // 移動平均のシフト値
//--- グローバル変数
int IndicatorHandle = 0; // インジケータのハンドル(識別子)
bool IsHedging = false; // ヘッジング口座フラグ
CTrade trade; // 取引操作クラスのインスタンス
//--- マジックナンバーの定義(識別子)
#define EA_MAGIC 18052018
//+------------------------------------------------------------------+
//| ポジションを開く条件を確認する |
//+------------------------------------------------------------------+
void CheckForOpen(void)
{
MqlRates rt[2]; // 過去2つのローソク足データを格納するための配列
//--- 新しいバーの始めのみで取引する
if (CopyRates(_Symbol, _Period, 0, 2, rt) != 2)
{
Print("CopyRates of ", _Symbol, " failed, no history");
return;
}
//--- ティックボリュームを確認する
if (rt[1].tick_volume > 1)
return;
//--- 移動平均値を取得する
double ma[1]; // 移動平均値を格納する配列
if (CopyBuffer(IndicatorHandle, 0, 1, 1, ma) != 1)
{
Print("CopyBuffer from iMA failed, no data");
return;
}
//--- シグナルの存在を確認する
ENUM_ORDER_TYPE signal = WRONG_VALUE; // シグナルの種類
//--- ローソク足が移動平均より高く開き、低く閉じた場合のシグナル
if (rt[0].open > ma[0] && rt[0].close < ma[0])
signal = ORDER_TYPE_BUY; // 買いシグナル
else if (rt[0].open < ma[0] && rt[0].close > ma[0]) // ローソク足が移動平均より低く開き、高く閉じた場合のシグナル
signal = ORDER_TYPE_SELL; // 売りシグナル
//--- 追加の確認を行う
if (signal != WRONG_VALUE)
{
if (TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol, _Period) > 100)
{
double price = SymbolInfoDouble(_Symbol, signal == ORDER_TYPE_SELL ? SYMBOL_BID : SYMBOL_ASK); // 取引価格を取得
trade.PositionOpen(_Symbol, signal, Lots, price, 0, 0); // ポジションを開く
}
}
}
//+------------------------------------------------------------------+
//| ポジションを閉じる条件を確認する |
//+------------------------------------------------------------------+
void CheckForClose(void)
{
MqlRates rt[2]; // 過去2つのローソク足データを格納するための配列
//--- 新しいバーの始めのみで取引する
if (CopyRates(_Symbol, _Period, 0, 2, rt) != 2)
{
Print("CopyRates of ", _Symbol, " failed, no history");
return;
}
if (rt[1].tick_volume > 1)
return;
//--- 移動平均値を取得する
double ma[1]; // 移動平均値を格納する配列
if (CopyBuffer(IndicatorHandle, 0, 1, 1, ma) != 1)
{
Print("CopyBuffer from iMA failed, no data");
return;
}
//--- ポジションがすでに選択されているか確認する
bool signal = false;
long type = PositionGetInteger(POSITION_TYPE); // ポジションの種類を取得
//--- ショートポジションを決済する条件
if (type == (long)POSITION_TYPE_SELL && rt[0].open > ma[0] && rt[0].close < ma[0])
signal = true;
//--- ロングポジションを決済する条件
if (type == (long)POSITION_TYPE_BUY && rt[0].open < ma[0] && rt[0].close > ma[0])
signal = true;
//--- 追加の確認を行う
if (signal)
{
if (TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol, _Period) > 100)
trade.PositionClose(_Symbol, Slippage); // ポジションを閉じる
}
}
//+------------------------------------------------------------------+
//| 口座タイプ(ネッティングまたはヘッジ)を考慮してポジションを選択する |
//+------------------------------------------------------------------+
bool SelectPosition()
{
bool res = false;
//--- ヘッジ口座のポジションを選択する
if (IsHedging)
{
uint total = PositionsTotal(); // 全ポジションの数を取得
for (uint i = 0; i < total; i++)
{
string position_symbol = PositionGetSymbol(i); // ポジションのシンボルを取得
if (_Symbol == position_symbol && EA_MAGIC == PositionGetInteger(POSITION_MAGIC))
{
res = true;
break;
}
}
}
//--- ネッティング口座のポジションを選択する
else
{
if (!PositionSelect(_Symbol))
return (false);
else
return (PositionGetInteger(POSITION_MAGIC) == EA_MAGIC); // マジックナンバーを確認
}
//--- 実行結果を返す
return (res);
}
//+------------------------------------------------------------------+
//| エキスパート初期化関数 |
//+------------------------------------------------------------------+
int OnInit(void)
{
//--- 取引タイプ(ネッティングまたはヘッジ)を設定する
IsHedging = ((ENUM_ACCOUNT_MARGIN_MODE)AccountInfoInteger(ACCOUNT_MARGIN_MODE) == ACCOUNT_MARGIN_MODE_RETAIL_HEDGING);
//--- 正しいポジション制御のために取引操作クラスのオブジェクトを初期化する
trade.SetExpertMagicNumber(EA_MAGIC); // マジックナンバーを設定
trade.SetMarginMode(); // 証拠金モードを設定
trade.SetTypeFillingBySymbol(Symbol());// シンボルに基づいた執行タイプを設定
trade.SetDeviationInPoints(Slippage); // 許容スリッページを設定
//--- 移動平均指標を作成する
IndicatorHandle = iMA(_Symbol, _Period, MovingPeriod, MovingShift, MODE_SMA, PRICE_CLOSE);
if (IndicatorHandle == INVALID_HANDLE)
{
printf("Error creating iMA indicator");
return (INIT_FAILED);
}
//--- 初期化成功を示す
return (INIT_SUCCEEDED);
}
//+------------------------------------------------------------------+
//| エキスパートティック関数 |
//+------------------------------------------------------------------+
void OnTick(void)
{
//--- ポジションが既に開かれている場合は、決済条件を確認する
if (SelectPosition())
CheckForClose();
//--- ポジションを開く条件を確認する
CheckForOpen();
}
//+------------------------------------------------------------------+
//| テスタ関数 |
//+------------------------------------------------------------------+
double OnTester()
{
//--- カスタム条件最適化の値(高いほど良い)
double ret = 0.0;
//--- 取引結果を配列に入れる
double array[];
double trades_volume;
GetTradeResultsToArray(array, trades_volume);
int trades = ArraySize(array);
//--- 10取引未満の場合、肯定的結果がないことをテストする
if (trades < 10)
return (0);
//--- 取引あたりの平均結果
double average_pl = 0;
for (int i = 0; i < ArraySize(array); i++)
average_pl += array[i];
average_pl /= trades;
//--- 単一テストモード用のメッセージを表示する
if (MQLInfoInteger(MQL_TESTER) && !MQLInfoInteger(MQL_OPTIMIZATION))
PrintFormat("%s: Trades=%d, Average profit=%.2f", __FUNCTION__, trades, average_pl);
//--- 利益グラフの線形回帰を計算する
double a, b, std_error;
double chart[];
if (!CalculateLinearRegression(array, chart, a, b))
return (0);
//--- 回帰直線からグラフの偏差の誤差を計算する
if (!CalculateStdError(chart, a, b, std_error))
return (0);
//--- 傾向偏差の標準偏差を計算する
ret = (std_error == 0.0) ? a * trades : a * trades / std_error;
//--- カスタム条件最適化値を返す
return (ret);
}
//+------------------------------------------------------------------+
//| 取引の利益/損失の配列を得る |
//+------------------------------------------------------------------+
bool GetTradeResultsToArray(double &pl_results[], double &volume)
{
//--- 完全な取引履歴をリクエストする
if (!HistorySelect(0, TimeCurrent()))
return (false);
uint total_deals = HistoryDealsTotal(); // 全取引の数を取得
volume = 0;
//--- 証拠金を持つ配列の初期サイズを、履歴の取引数で設定する
ArrayResize(pl_results, total_deals);
//--- 取引結果を修正する取引のカウンター - 利益または損失
int counter = 0;
ulong ticket_history_deal = 0;
//--- 全ての取引を見る
for (uint i = 0; i < total_deals; i++)
{
//--- 取引を選択する
if ((ticket_history_deal = HistoryDealGetTicket(i)) > 0)
{
ENUM_DEAL_ENTRY deal_entry = (ENUM_DEAL_ENTRY)HistoryDealGetInteger(ticket_history_deal, DEAL_ENTRY); // 取引のエントリタイプを取得
long deal_type = HistoryDealGetInteger(ticket_history_deal, DEAL_TYPE); // 取引のタイプを取得
double deal_profit = HistoryDealGetDouble(ticket_history_deal, DEAL_PROFIT); // 取引の利益を取得
double deal_volume = HistoryDealGetDouble(ticket_history_deal, DEAL_VOLUME); // 取引の量を取得
//--- 興味があるのは取引操作のみである
if ((deal_type != DEAL_TYPE_BUY) && (deal_type != DEAL_TYPE_SELL))
continue;
//--- 損益を固定する取引のみ
if (deal_entry != DEAL_ENTRY_IN)
{
//--- 取引結果を配列に書き込み、取引のカウンターを増やす
pl_results[counter] = deal_profit;
volume += deal_volume;
counter++;
}
}
}
//--- 配列の最終サイズを設定する
ArrayResize(pl_results, counter);
return (true);
}
//+------------------------------------------------------------------+
//| 線形回帰を計算する y=a*x+b |
//+------------------------------------------------------------------+
bool CalculateLinearRegression(double &change[], double &chartline[], double &a_coef, double &b_coef)
{
//--- データが十分か確認する
if (ArraySize(change) < 3)
return (false);
//--- 蓄積されたチャート配列を作成する
int N = ArraySize(change);
ArrayResize(chartline, N);
chartline[0] = change[0];
for (int i = 1; i < N; i++)
chartline[i] = chartline[i - 1] + change[i];
//--- 線形回帰を計算する
double x = 0, y = 0, x2 = 0, xy = 0;
for (int i = 0; i < N; i++)
{
x = x + i;
y = y + chartline[i];
xy = xy + i * chartline[i];
x2 = x2 + i * i;
}
a_coef = (N * xy - x * y) / (N * x2 - x * x); // 傾きaを計算する
b_coef = (y - a_coef * x) / N; // 切片bを計算する
//--- 成功を示す
return (true);
}
//+------------------------------------------------------------------+
//| 指定されたaとbの平均二乗偏差誤差を計算する |
//+------------------------------------------------------------------+
bool CalculateStdError(double &data[], double a_coef, double b_coef, double &std_err)
{
//--- 誤差の平方和
double error = 0;
int N = ArraySize(data);
if (N <= 2)
return (false);
for (int i = 0; i < N; i++)
error += MathPow(a_coef * i + b_coef - data[i], 2);
std_err = MathSqrt(error / (N - 2)); // 標準誤差を計算する
//--- 成功を示す
return (true);
}






