-<PR>-
当サイトでは以下のFX業者をおススメいたします。
—————————————————————
この記事では、相場分析において、もっともよく使われてるといっても過言ではない移動平均線について書いていきたいと思います。
移動平均線を学ぶことは、市場のトレンドを読み解く能力を養うためのステップであり、これにより、市場の騒音を切り分け、より一貫性のある市場分析を行う基盤を築くことができます。
もちろん、移動平均線についての理解を深める事イコール、収益性の向上を保証するものではありません。
トレーディングにおいては、多くの要素が絡み合い、移動平均線の知識だけが成功への鍵ではない事は論を待たない所でしょう。
それでも、移動平均線の理解を深めることは、市場の傾向を見極める際の洞察力を高め、統計的なアプローチで市場の動向を解析するための基礎を固めることに繋がります。
MQL5を使ったEA開発に移動平均線を使用する際には、継続的な学習と経験を通じて、システムトレーダーは移動平均線の示す情報をどのようにEA開発に落とし込み、実際のシステムトレードに活かすかを反芻して考えることが大切です。
この作業は、人によっては最初「辛い」と感じることがあるかもしれませんが、実はシステムトレードにおける醍醐味であると思っています。
また、例えば、MT5でも組み込みインジケータとして提供されているボリンジャーバンドという指標は、中央の移動平均線と、その移動平均線から上下2本に描画された標準偏差で形成されているマルチバッファインジケータです。つまり、移動平均線を正しく理解していないとボリンジャーバンドが提供する情報も正しく読み解く事ができない、という事になります。
是非、楽しみながら読んで頂ければと思います。
※ボリンジャーバンドについては↓のリンクをご覧ください。
標準偏差については↓の記事で詳しく解説していますので、ご覧くださると幸いです。
移動平均線とは?
移動平均線(Moving Average, MA)とは、為替価格や株価などの時系列データにおいて、特定の期間にわたる平均値を連続的に結んだ線のことを指します。
移動平均線は、市場のトレンドを把握するために使用されます。例えば、価格が移動平均線を上回っている場合は上昇トレンド、下回っている場合は下降トレンドを示唆していると解釈されます。
また、短期の移動平均線が長期の移動平均線を上回ったり下回ったりする「ゴールデンクロス」や「デッドクロス」と呼ばれる現象は、それぞれ買いまたは売りのシグナルとされることがあります。
- 単純移動平均(Simple Moving Average, SMA)
- 指数平滑移動平均(Exponential Moving Average, EMA)
- 線形加重移動平均(Weighted Moving Average, WMA)
単純移動平均線(SMA)とは?
単純移動平均(SMA)は最も基本的な移動平均線です。
この後紹介するEMAやLWMAに比べて、すべての価格データを同じ重みで扱うため、最近の価格変動が過剰に重視されることなく、選択した期間全体の平均的な価格レベルを示します。
単純移動平均 (SMA) の計算式について
単純移動平均(SMA)は、特定の期間にわたる価格の算術平均を取ります。
その計算式は以下の通りです↓
単純移動平均 SMA の計算式:
SMA=(P1+P2+P3+⋯+Pn)/n
ここで、
- P1,P2,P3,…,Pn は期間 n におけるそれぞれの価格データを示します。
- n は移動平均を計算するために使用される期間の数です。
たとえば、5日間の単純移動平均(SMA)を計算する場合は、最新の5日間の終値の合計を5で割ります。これにより、その期間における価格の平均値が求められます。
例えば、ドル円相場における5日間の単純移動平均(SMA)を計算するには、過去5日間の終値をすべて合計し、その日数で割ります。
具体的な数値を使って説明しましょう。以下の5日間のドル円相場の終値を例に取ります。
- 1日目: 110円
- 2日目: 111円
- 3日目: 110.5円
- 4日目: 112円
- 5日目: 111.5円
これらの終値をすべて合計すると、110+111+110.5+112+111.5=555110+111+110.5+112+111.5=555 円です。
次に、合計した価格を日数(この場合は5日間)で割ります。
555円/5=111円
したがって、この5日間の単純移動平均(SMA)は111円となります。
単純移動平均のメリットについて。
単純移動平均(SMA)の長所は、そのシンプルさにあります。データを平滑化することで市場の一般的なトレンドを示し、トレーダーが価格の動向を理解するのに役立ちます。
平滑化とは?
平滑化とは、端的に言えば、「データの波をなめらかにする」という意味合いになります。
具体的には、為替相場のような変動が激しいデータから、不規則な動きを取り除いて、本質的な流れやトレンドをより明瞭にすることを目的としています。これにより、データの背後にある本当のパターンや傾向を簡単に理解することができます。
SMAは、以下のような点で他の移動平均線と比較して強さを発揮します。
- データの均一な扱い: SMAは過去の価格データを全て同じ重みで扱うため、市場のトレンドを示す際に一つの価格が他の価格に比べて過剰に影響を与えることがありません。これにより、市場の長期的なトレンドが明確になります。
- シグナルの明確さ: 他の移動平均線よりも計算がシンプルであるため、トレーダーは単純移動平均(SMA)が生成するシグナルを解釈しやすくなります。これは初心者にとって特に有益です。
- トレンドの確立における信頼性: 単純移動平均(SMA)は長期的なトレンドの確立を確認するのに役立ちます。
- 急激な価格変動に対する反応が鈍いため、実際に確固たるトレンドが存在する場合には、この特性が利点となります。
従って、為替相場で長期的な方向性を分析する場合に単純移動平均(SMA)は有用です。
例えばドル円が長期にわたり徐々に上昇傾向にあるとします。
このような場合、単純移動平均(SMA)はその安定した上昇トレンドを滑らかに表示し、トレーダーにはその傾向が継続していることを確認するための明確な視覚的手がかりを提供します。
急激な価格の跳ね上がりや落ち込みがあっても、単純移動平均(SMA)はこれらの一時的な変動を平滑化し、トレーダーが過度に反応することなく長期的なトレンドに基づいた判断を下すのを助けます。
総じて、単純移動平均(SMA)は安定したトレンドが存在する市場や、短期的な価格の騒音に惑わされずに分析を行いたいときに最適です。また、市場のノイズを排除して、より長期的な視点から市場分析を行いたいトレーダーにとっても有用なツールとなります。
単純移動平均の弱点について
その一方で、単純移動平均(SMA)は、選択した期間にわたる価格データすべてに同じ重みを与えるため、市場の急激な変動に対しては反応が遅れる傾向があります。
これは、単純移動平均(SMA)が最新の価格変動よりも、選択した期間内の全ての価格データを等しく考慮するからです。
たとえば、ドル円相場の5日間の単純移動平均(SMA)を考えます。最初の4日間は市場があまり変動せず、5日目に大きな価格の跳ね上がりがあったとします。
- 1日目: 110円
- 2日目: 110円
- 3日目: 110円
- 4日目: 110円
- 5日目: 120円
5日目までの単純移動平均(SMA)を計算すると、以下のようになります。
(110+110+110+110+120)/5=560/5=112円
この場合、5日目に大きな価格上昇があったにも関わらず、単純移動平均(SMA)は112円となり、この新しい価格変動を完全には反映していません。
なぜなら、単純移動平均(SMA)は過去4日間の価格と5日目の価格を同じ重みで計算に含めているため、1日目から4日目の安定した価格が平均値を引き下げているからです。
このように、単純移動平均(SMA)は最新のデータに同じ重みを与えるため、価格の急激な上昇や下降があった場合、それが平均値に完全に反映されるのは、その変動が計算期間の終わりに近づくにつれて徐々にです。そのため、市場のトレンドに対する反応が遅れるという欠点があります。
指数移動平均線(EMA)とは?
指数平滑移動平均(Exponential Moving Average, EMA)は、最近の価格データに重みをより多く置き、古いデータよりも新しいデータがEMAの計算においてより大きな影響を与えるように設計されています。これにより、EMAは市場の最新の動きに対して単純移動平均(SMA)よりも迅速に反応することができます。
指数平滑移動平均線(EMA)の計算式について
指数平滑移動平均線(EMA)の計算には、
が必要です。
平滑化定数は、指数平滑移動平均線(EMA)算出において新しい価格情報がどの程度影響を与えるかを決定する為のものです。この後詳しく説明します。
計算の具体例として、ドル円の為替レートを用い、10日間のEMAを求める場合を考えます。
最初のEMAの計算: 最初の10日間のドル円の終値がすべて分かっていると仮定し、その平均値を最初のEMAとします。
平滑化定数の計算: 10日間のEMAの場合、平滑化定数は 2/(期間の日数+1)となります。つまり、2/(10+1)=2/11です
平滑化定数とは?
平滑化定数とは、指数平滑移動平均線(EMA)を計算する際に使用される係数で、新しい価格情報が移動平均に与える影響の度合いを決定します。
指数平滑移動平均線(EMA)では、最新のデータ点により大きな重みを与えることで、価格の最近の動きに敏感に反応するように設計されています。
平滑化定数の値は、( 2/{N+1} ) で表されることが多いです。ここで ( N ) は移動平均を計算するための期間の数です。
平滑化定数 ( k ) は ( 0 ) から ( 1 ) の間の値を取り、( k ) の値が大きいほど最新の価格に与える重みが増え、移動平均は価格の変動に対してより敏感になります。逆に ( k ) の値が小さいと、より滑らかな移動平均が得られ、価格の短期的な動きにはあまり影響されません。
新しいEMAの計算: 11日目の終値が新たに得られたと仮定します。この新しい価格を使って、新しいEMAを次のように計算します。
新しいEMA=(新しい価格−前日のEMA)×平滑化定数+前日のEMA
ここで、11日目の終値が116円だったと仮定し、最初のEMAEMAが112円だったとしましょう。
新しいEMA=(116−112)×(2/11)+112
=4×2/11+112
=8/11+112
=0.727+112
=112.727円
したがって、11日目のEMAは約112.727円となります。
この計算式の解釈は次のようになります:
- 「今日の価格 – 昨日のEMA」は、今日の価格が昨日のEMAからどの程度変動したかを示しています。
- この変動に平滑化定数を掛けることで、変動のうちどの程度を今日のEMAの計算に取り入れるかを決定します。この定数が大きいほど新しい価格の影響が大きくなります。
- 最後に、その結果に「昨日のEMA」を加えることで、今日のEMAを得ます。
この計算を毎日繰り返すことによって、各日のEMAを更新し続けることができます。
EMAがSMAに比べて最新の価格に重みを置いている理由
指数平滑移動平均線(EMA)が単純移動平均(SMA)に比べて最新の価格に重みを置いている理由は、指数平滑移動平均線(EMA)の計算方法が最新の価格変動をより強く反映するように設計されているからです。
単純移動平均(SMA)の弱点が、市場の急激な変動に対しては反応が遅れる傾向がある、という事は既に書いた通りですが、指数平滑移動平均線(EMA)はその弱点を補うもの、といえるでしょう。
単純移動平均(SMA)は過去の一定期間の価格を同じ重みで平均を算出します。
例えば、10日間の単純移動平均(SMA)では、10日前の価格も昨日の価格も同じ重みで計算に入ります。それに対して、指数平滑移動平均線(EMA)は「重み付け」という工夫をしています。
指数平滑移動平均線(EMA)では、最新の価格と前日のEMAとの差に「平滑化定数」という比率をかけて、前日のEMAに足します。この平滑化定数が、新しい価格により大きな重みを与える役割を果たしています。
例えば、平滑化定数が0.2だとしましょう。価格が昨日に比べて上がった場合、その増加分の20%だけが新しい指数平滑移動平均線(EMA)の計算に使われます。
この増加分は、前日のEMAに足されて、新しいEMAが計算されます。このプロセスを繰り返すことで、最新の価格変動がEMAに継続的に影響を与え、結果として最新の価格に重みを置いた平均が形成されるのです。
わかりやすく言うと、指数平滑移動平均線(EMA)は「最新のニュースは古いニュースより重要」という考え方に基づいています。
最新の価格が反映されると、指数平滑移動平均線(EMA)はすぐに動き、新しいトレンドや変化に敏感になります。古い価格は次第に忘れ去られ、新しい価格がより強く影響を与えることになるのです。
指数平滑移動平均線(EMA)の弱点は?
指数平滑移動平均線(EMA)の弱点は、以下の点が挙げられます。
価格の急変に対する過敏反応: 指数平滑移動平均線(EMA)は最新の価格変動に重みを置くため、市場の急激な上昇や下降に対して過敏に反応することがあります。
これは、短期的な「ノイズ」と実際のトレンド変化を区別しづらくすることがあり、誤ったトレードのシグナルを引き起こす可能性があります。
価格反転時の遅延: 価格が方向を変えたとき、指数平滑移動平均線(EMA)はその変化に追いつくために時間がかかることがあります。この遅れは、特に市場が方向性を持たずにレンジ内で動いているときに顕著です。
トレンドの終わりにおける遅れ: トレンドが終わる際も、指数平滑移動平均線(EMA)はトレンドの終焉を示すのに遅れが生じることがあります。これにより、ポジションを閉じるのに最適な時期を見逃すリスクがあります。
複雑な計算: 指数平滑移動平均線(EMA)の計算は単純移動平均(SMA)よりも複雑であり、相場分析に誤認が生じる可能性があります。
線形加重平均線(LWMA)とは?
線形加重平均線(LWMA)は、最新の価格により大きな重みを置いて計算される移動平均です。
線形加重平均線(LWMA)もまた、先ほど解説したEMAと同様に、単純移動平均(SMA)に比べて最近の価格により大きな重みを置く移動平均線になるのですが、EMAとは異なる計算方法を使用します。
「線形」
※「線形」という言葉はいくつかの意味を持ちますが、移動平均における線形とは、最新のデータに割り当てる重みが時間に関して直線的(つまり一定の割合で)減少することを意味します。
例えば、線形加重平均線(LWMA))では、最新の価格には最大の重みを、過去に遡るにつれて重みが一定の割合で減少するように割り当てられます。
この減少は直線的な傾向を持ち、グラフに描くと直線になる特性があります。詳しい事はこの後すぐに説明するので、そちらをご覧ください。
線形加重平均線(LWMA)の計算式について
線形加重平均線(LWMA)の計算は次のようなステップで行います:
- 各価格に重みを割り当てる: 最新の価格には最も大きな重みを割り当て、過去に遡るにつれて重みを減少させます。たとえば、5日間のLWMAを計算する場合、最新の日には重み5を、その前の日には重み4を、というように割り当てます。
- 重み付き価格の合計を計算する: それぞれの価格に割り当てた重みを掛け合わせ、その合計を求めます。
- 重みの合計を計算する: 使用したすべての重みを合計します。
- 重み付き価格の合計を重みの合計で割る: 2で求めた重み付き価格の合計を3で求めた重みの合計で割り、LWMAを求めます。
具体的な計算例を見てみましょう。ドル円の為替レートに対して5日間のLWMAを計算する場合を想定します。以下は5日間のドル円の終値とします。
- 1日目: 110円
- 2日目: 111円
- 3日目: 112円
- 4日目: 113円
- 5日目: 114円
これらの価格に対して、1日目が重み1、2日目が重み2、というように割り当てていきます。5日目は最新の価格なので重み5を割り当てます。
重み付き価格の合計を計算すると:
110円×1+111円×2+112円×3+113円×4+114円×5
これを計算すると: 110+222+336+452+570=1690円
重みの合計は: 1+2+3+4+5=151+2+3+4+5=15
となります。
重み付き価格の合計を重みの合計で割ります: 1690円/15=112.67円
したがって、この5日間のLWMAは約112.67円となります
EMAとLWMAの共通点と相違点について
指数平滑移動平均線(EMA)と線形加重平均線(LWMA)は、どちらも最新のデータに重みをより多く与えるという共通点があります。
ただし、重みの割り当て方に違いがある為、当然形成される線にも、若干の傾向の違いが見られます。
端的に言うと、EMAはLWMAに比べて価格変動に対する反応がやや緩やかです。
LWMAは線形の重み付けにより、価格の最新の変動に対してより直接的に反応します。
これは指数平滑移動平均線(EMA)とLWMAの計算式の違いを比較すると、何となく理解して頂けるのではと思います。
EMAの場合、指数的に減少する重み(平滑化定数)を過去の価格データに割り当てるため、最新の価格変動は計算に大きく影響しますが、過去の価格データも無視されずにある程度影響を与え続けます。
つまり、過去のEMAの値が新しいEMAの計算に連続的に組み込まれるため、価格の急激な変化がEMAの値を急には変更しにくい構造になっています。これにより、EMAは価格の変動に対して滑らかで緩やかな反応を示すことが多いです。
一方で、LWMAは最新のデータに線形の重み付けを施し、古いデータへの重みが直線的に減少します。LWMAでは各価格に直接的な線形重みを掛け合わせるため、最新の価格の影響がより強く表れ、価格変動に対して素早く反応する傾向があります。
要するに、EMAの計算には「平滑化」という概念が含まれており、これが過去の価格データの影響を持続させ、価格の急激な変動に対する反応を緩和します。これはEMAがトレンドを滑らかに追従するのに役立ちますが、その結果として反応速度がLWMAよりも若干遅くなるのです。
まとめ
今回は移動平均線について解説しました。
まず最初にそもそも移動平均線とは何か?という大前提から説明し、移動平均線にもいくつかの種類がある事をお伝えした上で、その内訳である
それぞれの、特徴・計算式・違いなどについても説明をしました。
詳しくは単純移動平均(SMA),指数平滑移動平均線(EMA),線形加重平均線(LWMA)それぞれの項を見て頂きたいのですが、端的に言うのであれば単純移動平均(SMA)は指定期間におけるデータをを均等に扱うのに対し、指数平滑移動平均線(EMA)と線形加重平均線(LWMA)はより直近のデータに重きを置いた仕組みになっています。
そして、指数平滑移動平均線(EMA)と線形加重平均線(LWMA)を比較すれば、線形加重平均線(LWMA)は指数平滑移動平均線(EMA)よりも、直近のデータを重視したものと言えます。
↓のグラフをご覧ください。
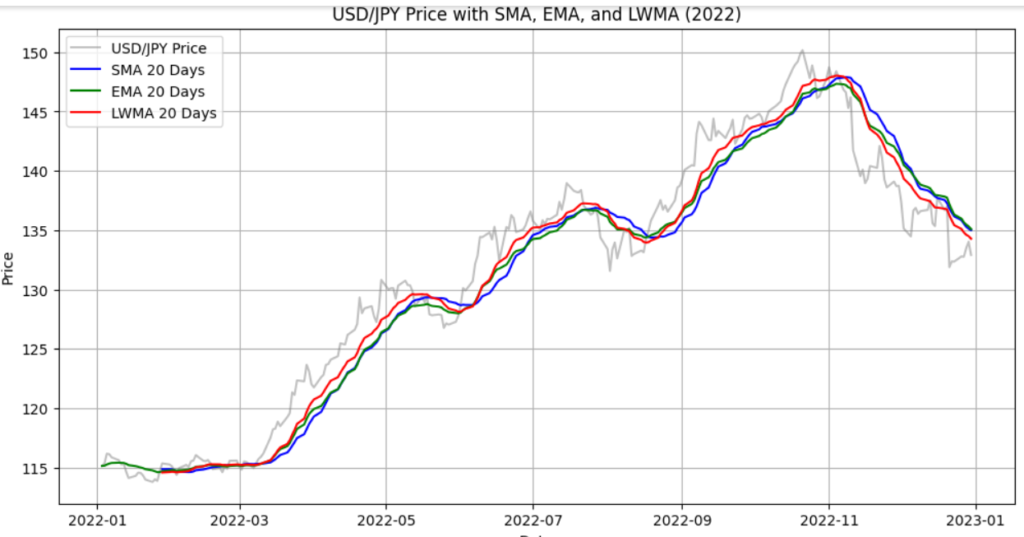
こちらのグラフは、シミュレートされたUSD/JPY(ドル円)の価格推移を示しています。価格データは2022年1月1日から12月31日までの期間にわたって作成され、その期間における20日間の単純移動平均(SMA)、指数平滑移動平均線(EMA)、線形加重平均線(LWMA)が描かれています。
・グレーの線はシミュレートされたUSD/JPYの価格を示しています。
・青色の線は20日間のSMAを、緑色の線は20日間のEMAを、赤色の線は20日間のLWMAをそれぞれ表しています。
ご覧いただくと、直近のデータに最も重きを置いているLWMAが一番早くトレンドに反応し、EMAがそれに追随する形、SMAの反応が一番ゆっくりである事が分かります。これは反応の早い遅いそれ自体に良い悪いがある訳ではなく、開発するEAの戦略によってその良しあしは変わってきます。
MQL5を利用したEA開発にあたり、そのロジックに移動平均線を取り入れる際にはその違いを加味すると良いでしょう。
例えば、長期的なトレンドを把握すればよい長期保有型トレンドフォローEAであれば、単純移動平均(SMA)を採用する…逆にデイトレードやスキャルピングを視野に入れたEAを開発したいのであれば指数平滑移動平均線(EMA)や線形加重平均線(LWMA)を採用する…といった具合です(あくまで例であり、推奨している訳ではありません)
今回は以上とさせていただきます。
最後までお読みいただきありがとうございました。
※移動平均線を使ったEA作成に関しては、以下の記事もご参照ください。
・【MQL5】5分で書ける、パーフェクトオーダーの記述【EAの作り方】
※MQL5において、移動平均線情報を取得するiMA関数については↓のリンクをご覧ください。
—————————————————————
-<PR>-
MQL5を使って自作したEAをシステムトレードに利用するには、取引プラットフォームとしてMT5を提供しているFX会社に口座を開設しなくてはいけません。
当サイトでは以下のFX会社での口座開設・EA運用をおススメしています。
おススメする理由の詳細につきましては、各FX会社について解説する記事を書いておりますので、下記のリンク記事を参考にしていただければと思います。
※外為ファイネストに関する記事は↓をご覧ください。
※アヴァトレードジャパンに関する記事は↓をご覧ください。
※フィリップ証券に関する記事は↓をご覧ください。











コメント